
最近Processingで久々に遊んでいます。以前はライブラリを組み合わせて”わーできたー”位のことをやっておりましたが、最近基礎力を身につけたいと思って幾何学的なことも軽く学んでいます。
さて、文化というかよく見かけるProcessingのサンプルは縦に長ーくて変数の値がなんだったのか途中から忘れてしまうようなものが多いです。
例えば折れ線グラフを書くようなケースの場合、
統計情報をデータソースから取得する > X軸、Y軸を描く > X、Yの最大値を求めてスケールを決める > ちょうどいい単位に目盛りを引く > 折れ線グラフを描く
といったステップを分けて踏むとコードがすっきりするのですが、一方でX軸、Y軸のディスプレイ上の座標や、XやYの最大値やなどの変数はスケッチを通して保持したいもので、そのことが縦に長ーいプログラムだとコードを複雑にしがちです。Proceccingの世界だとおそらく一回使い切りのプロジェクトもしくは次回使うことがあってもコピペして修正すれば割とすんでしまうようなことが多いのかもしれません。
でも、やっぱり再利用可能な部品を作りたいですね。コードを関数に区切ると変数のスコープが狭まるのでミニマムなことにフォーカスできます。
下記のコードでは最初に以下の引数で図形を調整できるものという条件を固持するものとして書きました。
- 正N角形のN
- 半径
# どこから読めばいいのか?
まずはsetupとdrawを読んでください。特にdrawを読むことで大まかな流れがつかめるでしょう。
// 半径200pxの6角形を描く polygon = new EquilateralPolygon(6, 200); // 頂点を取得 polygon.vertexes(); // 頂点を描く polygon.drawVertexes(); // 番号を描く polygon.drawIndexes();
肝になるところだけ軽く触れておきましょう。
# #xVertex, #vertexes()
vertexesは頂点の座標を集めています。
public float xVertex(int i, int extra) {
return cos(angles[i]) * (radius + extra);
}
public Coordinate[] vertexes() {
vertexes = new Coordinate[numVertexes];
float angleForSingleArc = 2 * PI / numVertexes;
for(int i = 0; i < numVertexes; i++) {
// Sum up angles
angles[i] = HALF_PI - angleForSingleArc * i;
float x = xVertex(i, 0);
float y = - yVertex(i, 0);
vertexes[i] = new Coordinate(x, y);
}
return vertexes;
}
ある頂点のX座標は三角関数を使って以下のように求められます。sinとcosを使った辺の長さの求め方
# xVertex
cos(角度) * 半径
y座標はsinを使って以下のように求められます
# yVertex
sin(角度) * 半径
xVertex中では半径だけを使ってって計算しています。これは円の中心を起点の0,0としてその差分を座標として計算し描写しているからです。ただ描写する正確な座標ははプログラマが意識しないですむようにtranslate関数であらかじめずらしています。
# 拡張点の座標の求め方
angles[i] = HALF_PI - angleForSingleArc * i;
PIはπを意味するあらかじめProcessingに用意された定数です。上記のx, yの関数で角度が0の場合processingは右端になります。そこから始まって反時計回りに角度を表します。
0 => QUARTER_PI(45度) => HALF_PI(90度) => PI(180度) => 2 * PI(360度)
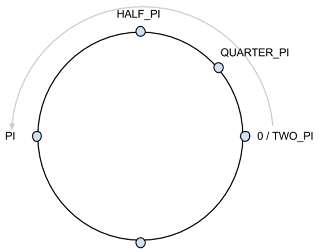.png)
一つずつの頂点について図の一番上を起点としてそこからの角度をi毎に取得します。時計回りに点を配置することにしたので マイナスを付けて逆方向に回転させます。
angles[i] = HALF_PI - angleForSingleArc * i;
# なぜOOPを使ってシンプルに書くのが難しいのか?
なぜProcessingではOOPをつかってシンプルに書くのがむずかしいのでしょうか?コードを書いていて思ったことがあります。
- 文脈依存の関数が多い
例えばこのコードに出てくる以下のようなコードは文脈依存です
fill(BLACK);
text(i, vertexes[i].x, vertexes[i].y);
noFill();
noLoop()
translate(DISPLAY_WIDTH / 2, DISPLAY_HEIGHT / 2)
全て後述の処理に影響します。
- 一個のループに何でもまとめてしまう
計算量が気になってしまい一個のループに何でもまとめてしまうのでそのループを含む関数がいろんなことをやってしまいがちです。lambdaを使ってループのある関数内で座標計算や描写などを遅延評価させてあげればいいんですかね。
http://www.oracle.com/webfolder/technetwork/tutorials/obe/java/Lambda-QuickStart/index.html?cid=7180&ssid=3993398328344#section2
以上、久々のJava勉強になりました。